This linked YouTube video (factoring 35, 130, 72) shows the analysis of three factorization diagrams: 35, 130, and 72. The numbers are listed in increasing level of difficulty. The more factors in the factorization, the more difficult it is to analyze the diagram. Thirty-five can be factored as 7 x 5; 130 can be factored as 2 x 13 x 5; and, 72 can be factored as 2 x 2 x 3 x 3 x 2. There are many ways to factor these numbers with a corresponding number of diagrams. I will go through one example for each number. In my class, we use iPads and the Doceri app to create and analyze these diagrams. The videos are created using Doceri, Keynote, and iMovie. An important aspect of this work is that the software is freely available. My students were given an iPad so with the free software, they were able to do this work.

To begin a factorization analysis of a number, look for equal groups of dots in the diagram. The number of equal groups is the first factor in the corresponding multiplication problem. Thirty-five begins with 7 equal groups; and, both 130 and 72 begin with 2 equal groups. Thirty-five has 5 dots within each of the seven

groups. Its factorization is complete.  130 has a set of thirteen nested groups within each of the two large groups. There are 5 dots within each of the smaller 13 groups. Thus, the factorization of 130 is 2 large groups of 13 smaller groups: 2 x 13 = 26 of these smaller groups. Within each of these 26 smaller groups are 5 dots: 26 x 5 = 130 total dots.

2 x 13 x 5 =
26 x 5 =
130 dots

Within the factorization of 130 is a factor of 10: 2 x 5. It would be useful for students to factor and diagram 10 x 13 as 2 x 5 x 13 or 5 x 2 x 13 and compare these diagrams to the original 2 x 13 x 5. This activity would provide experience with 10 groups of 13 (multiplying by 10), or, if the order was changed to 13 x 2 x 5 or 13 x 5 x 2, the drawing becomes 13 groups of 10. These different drawings of the same set of factors build a conceptual understanding of factors, multiplication, and place value (grouping by tens) as well as the commutative property. These simple changes result in vastly different diagrams.

The factorization of 72 also begins with 2 equal groups. Seventy-two is the most difficult  three numbers, even with factors of only twos and threes! Begin with the two large

groups and, then, loop two smaller groups within each of these larger groups: 2 x 2 = 4 groups (blue). There are 3 smaller groups within each blue group (red). There is a total of 12 red groups (2 x 2 x 3 = 12). Within each red group are three smaller groups (green) for

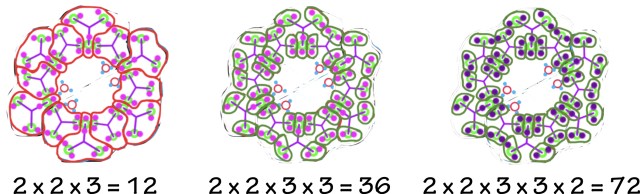
a total of 36 very small groups (2 x 2 x 3 x 3 = 36). Finally, there are two dots within each of these very small groups that equal the 72 total dots (2 x 2 x 3 x 3 x 2 = 72).

I will continue to analyze student diagrams, create my own diagrams, and provide both video and text explanations. These ideas take much time and effort to build understanding. The main thought is that students have a way to conceptualize theses ideas.